Fadenpendel

Der Versuch

An ein Fadelpendel werden nacheinander verschiedene Gewichte gehängt. Die Periodendauer, d.h. die Zeit, die es dauert, bis das Pendel bei einer Schwingung wieder am Startpunkt der Auslenkung angekommen ist, ist immer gleich, unabhängig von der Masse des Gewichts.

Informationen für Interessierte

In der Physik können schwingende Systeme häufig als sogenannte Harmonische Oszillatoren beschrieben werden. Ein Oszillator bezeichnet ein schwingungsfähiges System (von lat. oscillare: schaukeln, schwingen), harmonisch wird dabei dann ein sinusförmiger Bewegungsablauf bezeichnet, der einem linearen Kraftgesetz folgt:
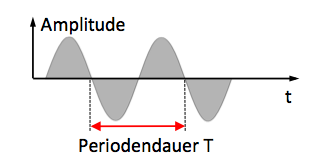
Diese Bewegungsform wurde offenbar als besonders gleichmäßig , „von Harmonie geprägt“, angesehen. Beim Fadenpendel läßt sich dann die Auslenkung, die Amplitude, des schwingenden Körpers als Funktion der Zeit beobachten. Den Abstand der gleichen Schwingbewegung bezeichnet man dabei als Periodendauer. Das Fadenpendel wurde schon von Galileo Galilei genauer untersucht. Er fand, dass die Periodendauer des Pendels nicht von der Auslenkung oder dem Gewicht des Pendels, sondern nur von dessen Länge abhängt.

Informationen für Fortgeschrittene

Beim Fadenpednel wird sowohl die Rückstellkraft, die bei einer Auslenkung die Rückkehr in die Ruhelage bewirkt, als auch die Spannung des Fadens durch die Gewichtskraft des angehängten Gewichts bewirkt. Die eine Komponente der Gewichtskraft wirkt in Richtung des Pendelfadens. Diese ist für die Schwingung nicht wichtig, sie hält aber den Faden straff und legt somit die Bahnkurve als Kreisbahn fest. Die andere Komponente verläuft tangential zur Bahnkurve und wirkt als Rückstellkraft.

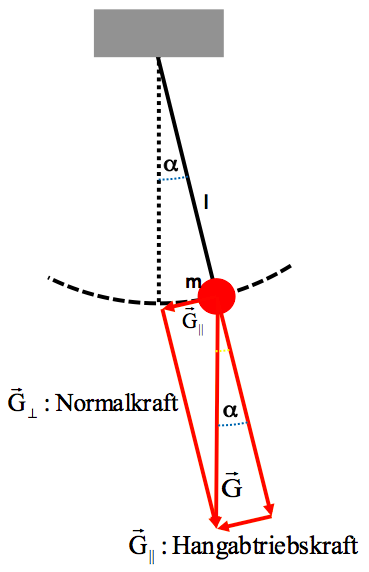
Will man nun die Bewegungsgleichung aufstellen, so ist zu beachten, dass die Wegänderung nur entlang dem Kreisbogen mit Radius l erfolgen kann. Dazu führt man ein gekrümmtes Koordinatenachse ein, die Koordinate ist der Kreisbogenabschnitt s, vom Ruhepunkt des Pendelkörpers aus gemessen. Man erhält eine nicht-lineare, homogene Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, die nicht so einfach zu lösen ist. Man kann aber versuchen, die gleichung zu vereinfachen, indem man eine Näherung für kleine Winkel macht. (Die sogenannte Taylorreihendarstellung der Sinusfunktion für kleine Winkel). Die Linearisierung ist, wie gesagt, nur gültig für kleine Winkel und man erhält eine lineare Differentialgleichung zweiter Ordnung, die einfacher zu lösen ist. Man erhält dann für die Periodenlänge als Lösung dieser Gleichung:

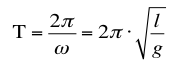
ω beschreibt die Kreisfrequenz, l die Fadenlänge und g die Erdbeschleunigung. Man beachte, dass T von der Masse des Pendelkörpers unabhängig ist! Allerdings gilt dies nur für kleine Winkelauslenkungen.

Text: Henner Büsching